4. TAŞIT PERFORMANS HESAPLARI

[4.1] 

buradaki S kayma faktörüdür.

En büyük vitesteki maksimum hız eğer taşıt üzerindeki harekt dirençleri biliniyorsa hesaplanabilir. 2. Bölümde elde edilen taşıt genel hareket denklemini (denklem 2,1) tekrar incelediğimizde hızın maksimum değerini alması için d²x/dt² teriminin sıfıra eşit olması gereklidir. Diğer bir deyişle taşıtın ürettiği gücün tamamının hareket dirençlerine karşı kullanıldığı noktadır. Buna göre;

[4.2]

[4.3] olur.

Bu ifadede taşıtın maksimum hızından bahsedildiğine göre taşıt düz yolda ve römorksuz olarak düşünülmektedir. Daha öncede bahsedildiği gibi bu denklem bize toplam çeki kuvveti ile hareket dirençlerinin kesiştiği noktayı vermektedir.

4.2 nolu denklem çözüldüğünde taşıtın maksimum hızı;

[4.4]

2. bölümdede bahsedildiği gibi maksimum çeki kuvvetini sınırlayıcı iki etken vardır. Dolayısıyla maksimum taşıt hızını da sınırlayan iki etken vardır. Buna göre maksimum taşıt hızıda ayrı iki çeki kuvvetine göre hesaplanan hızlardan küçük olanıdır. Bu durum en iyi Şekil 4.1’de görülebilir. Bu grafikte motora bağlı maksimum taşıt hızının yanı sıra yol adezyon sınırıda belirtilmiştir. Eğer toplam direnç kuvvetleri ile çeki kuvveti eğrisi adezyon sınırının üzerinde bir noktada kesişiyorsa bunu gerçekleşme imkanı olmadığından toplam direnç kuvveti ile adezyon sınırını kesiştiği nokta maksimum hız olarak belirtilir.

Şekil 4.1: Çeki kuvveti, adezyon sınırı ve direnç kuvvetleri.

4.3 nolu denklem hareket dirençlerinin ve özelliklede aerodinamik direncin taşıt hızına ne kadar etkili olduğunu göstermektedir. Yukarıda anlatılan maksimum taşıt hızı analizinde hareket dirençleri kısmında incelenen aerodinamik kaldırma kuvveti dikkate alınmamıştır. Aerodinamik kuvvetin taşıt hızı üzerindeki etkisi oldukça karmaşıktır. Kaldırma kuvveti lastik yuvarlanma direncini ve aks yüklerini oldukça etkilemektedir. Örneğin Formüla 1 yarışlarında kullanılan taşıtların normal ağırlığı 750 kg olmasına karşın, negatif kaldırma kuvveti sayesinde 250 km/h hıza çıktıklarında akslardaki toplam normal yük 2500 kg gibi yüksek değerlere çıkmaktadır. Bu ağırlık artışı hem çeki kuvvetinin adezyonla sınırlanmasını önlemekte hemde taşıtın manevra kabiliyetini arttırmaktadır. Buna karşın şu anda piyasadaki çoğu otomobilin aerodinamik kaldırma kuvveti pozitif, yani yukarı doğrudur.

Eğer taşıtın motor gücünün %70’ini kullandığı kabulünü yaparsak, toplam gücün toplam hareket direncine eşit olduğu durum için maksimum hız aşağıdaki gibi hesaplanabilir:

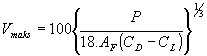[4.5].

4.2 İvmelenme Performansı

Binek taşıtların ivme performansı genellikle bir hızdan daha yüksek bir hıza çıkmak için geçen süre olarak verilir. Bazen bu süreye ilaveten katedilen mesafede verilebilir. Toplam çeki kuvveti için verilen iki ifade eşitlenip integrali alınırsa;

[4.6]

[4.7]

Bu ifadedeki toplam çeki kuvvetini taşıt hızına bağlı olarak yazmak istersek

[4.8] denkleminde motor hızı yerine yazılabilir. Bunun yanısıra daha önce çıkartılan yaklaşık motor gücü eğrisinin analitik çözümüde aşağıdaki şekilde yeniden yazılabilir.

[4.9]

burada;

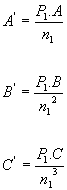[4.10]

4.8 ve 4.9 denklemlerini birleştirdiğimizde:

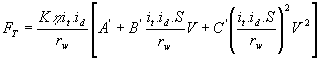[4.11] elde edilir. 

Net kuvveti bulmak için bu çeki kuvvetinden direnç kuvvetleri çıkarılır:

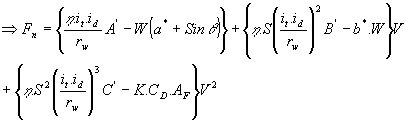[4.12]

Bu net çeki kuvvetini hıza bağlı bir polinom olarak ifade edilebilir:

[4.13]

burada;

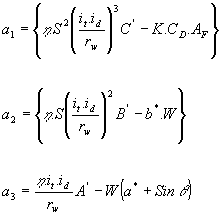[4.14]

4.7 nolu denkleminde F_n yerine 4.13 nolu denklemde elde edileni yazıp integrali alındığında hızlanma için geçen süre bulunabilir:

;

,

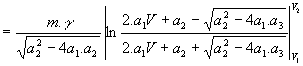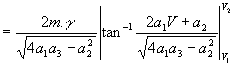 , [4.15]

Bu süre içerisinde katedilen mesafeyi bulmak için dt yerine ds/V yazılır ve integrali alınır.

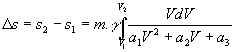
[4.16]

Taşıtların ivme performansı genellikle taşıtın sıfırdan 100 km/sa’e kadar ne kadar zamanda ulaştığı ile verilir. Bunun yanı sıra özellikle binek otomobiller için en büyük viteste, düşük hızlardan yüksek hızlara hızlanma zamanıda ek olarak verilir ve buna taşıtın elastikiyeti denir.

Bazı taşıtların maksimum hızları ve ivme performanslarını içeren tablo Ek-1 de verilmiştir.

4.3 Vites Değiştirme Sırasındaki Hız Kayıpları

Taşıtın ivmelenmesin sırasında her vites değiştirme esnasında bir miktar hız kaybı meydana gelir. Bu hız kaybının sebebi taşıtın her vites değiştirme sırasında aktarma organlarının motorla bağlantısının kesilmesi ve bu süre boyunca direnç kuvvetlerinin etkisi altında yavaşlamasıdır.

Bu hız kaybı 4.15 nolu denklemden deneme yanılma yoluyla hesaplanabilir. Fakat bazı kabuller yapılarak çıkarılan analitik çözüm daha basit ve daha hızlıdır, bunun yanı sıra yapılan hata miktarıda hız kayıpları az olduğu sürece oldukça düşüktür. Vites değiştirme sırasında direnç kuvvetlerinin sabit kaldığı kabul edilirse, taşıtın yavaşlaması;

[4.17]

burada;

V₁, V₂: vites değiştirmeden önceki ve sonraki taşıt hızları

D t_s: vites değiştirme sırasında geçen süre

m.g : taşıtın ağırlığı ve atalet kuvvetlerinin etkisinin (kütle faktörü) çarpımı

: V₁ hızındaki toplam direnç kuvvetleridir.

Denklem 4.17’ye göre vites değiştirme esnasında katedilen mesafe:

[4.18] olur.

Yeterli sürücülük tekniklerine sahip bir sürücü için tipik vites değiştirme oranları Tablo 4.1’de verilmiştir.

Tablo 4.1: Kalifiye bir sürücü için vites değiştirme süreleri.

4.4 Tırmanma Yeteneği

Taşıtın sabit bir hız ile tırmanabileceği en büyük eğime taşıtın tırmanma yeteneği adı verilir. Taşıtın eğim kapasitesi 1.Viteste elde eldilen değerle ifade edilir, çünkü taşıt 1. Viteste en büyük çeki kuvvetini üretir. Bu esnada taşıtın net çeki kuvveti sıfırdır.

Taşıtların tırmanma yeteneği iki nedenden dolayı sınırlıdır. Bunlar:

1. Adezyonla sınırlı eğim kapasitesi: Çeki tekerlekleri ile yol arasındaki adezyon katsayısı, lastiklerin gerekli torku kaymadan iletebilmesi anlamına gelir. Bunun için buna kayma sınırlı eğim kapasiteside denir.
2. Motor gücü ile sınırlı eğim kapasitesi: Taşıt motorunun üretebildiği maksimum çeki kuvveti ile tırmanılabilecek en büyük eğim anlamına gelir.

Taşıtın eğim kapasitesi ile ilgili analiz yapılırken yukarıdaki iki duruma göre de hesap yapılmalı ve çıkan değerlerden küçük olanı taşıtın eğim kapasitesi olarak tayin edilmelidir.

4.4.1 Adezyonla Sınırlı Eğim Kapasitesi

Taşıt ivmesinin sıfır olduğu ve başsallama momentinin olmadığı durum için Şekil 2.2’deki yatay kuvvetler toplanıp, yolun adezyon durumunun taşıyabileceği kuvvete eşitlenerek taşıtın eğim kapasitesi bulunabilir.

4.4.1.1 Önden Çekişli Taşıtta Adezyonla Sınırlı Eğim Kapasitesi

Eğer m yolun adezyon katsayısı ise.

[4.19]

Bu eşitlikte ilgili değerleri yerine koyarsak, verilen adezyon kuvveti için taşıtın tırmanabileceği açıyı bulmuş oluruz:

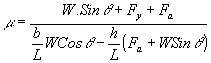
bu eşitliğin pay ve paydası W.Cosq ile bölünürse

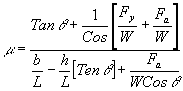
son olarak yukarıdaki denklemde yuvarlanma direnci yerine değerini yazarsak:

bu denklemden taşıtın eğim kapasitesi aşağıdaki gibi bulunabilir:

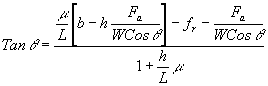[4.20]

Pratik olarak maksimum eğim kapasitesinin hesaplanması için Cosq ’nın değeri “1” olarak alınabilir. Bunun yanısıra eğim kapasitesi 1. Viteste hesaplandığı için hız düşüktür ve aerodinamik direnç kuvvetleri de sıfır olarak alınabilir. Bu durumda eğim kapasitesi:

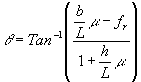[4.21] olur.

4.4.1.2 Arkadan Çekişli Taşıtta Adezyonla Sınırlı Eğim Kapasitesi

önceki bölümde önden çekişli taşıtta uygulanan aynı prosedürle, arkadan çekişli taşıtın eğim kapasitesi aşağıdaki şekilde elde edilebilir:

[4.22]

ve

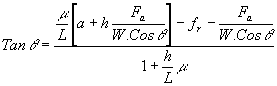[4.23]

önden çekişli taşıtta olduğu gibi bazı kabuller yapıldığında arkadan çekişli taşıtın eğim kapasitesi pratik olarak.

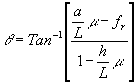[4,24]

4.4.1.3 Dört Tekerden Çekişli Taşıtta Adezyonla Sınırlı Eğim Kapasitesi

[4,25]

[4.26]

[4.27]

4.21, 4.24, 4.27 nolu denklemler karşılaştırıldığında dört tekerden çekişli bir taşıtın önden ve arkadan çekişli taşıtlara göre çok üstün olduğu görülür. Bunun yanında arkadan çekişli taşıtın eğimden dolayı oluşan yük transferinden dolayı önden çekişli taşıta nazaran daha yüksek eğim kapasitesine sahip olacağı görülmektedir.

4.4.2 Güç ile Sınırlı Eğim Kapasitesi

Şekil 2.2’deki kuvvet dengesine geri dönersek;

burada a₃=a₃^’-W.Sinq yazılırsa

[4.28]

[4.29] olarak elde edilir.

Bu maksimum eğimde taşıtın hızı da aşağıdaki şekilde hesaplanır

[4.30]

bu hız eşitliği 4.29 nolu denklemde yerine yazılırsa, güçle sınırlı eğim kapasitesi:

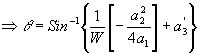[4.31]

maksimum tork noktasındaki taşıtın hızını bularak güçle sınırlı eğim kapasitesi için yaklaşık ama basit bir formül bulabiliriz. Bunun için maksimum eğimde;

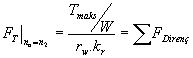
[4.32]

Yokuş üzerinde durmakta olan bir taşıtın eğim kapasitesi hesabının formülasyonu kolay değildir. Bu durumu gözönünde tutmak için yapılan eğim kapasitesi hesaplarından %5’lik bir değer çıkarılmalıdır.