Bir taşıt hareket halindeyken yere göre bir rölatif hızı vardır. Hava hareketsiz olduğunda ve rüzgar olmadığında taşıt yere ve aynı zamanda havaya gire eşit rölatif hıza sahiptir. Fakat rüzgar olduğunda, yani hava yere göre bir rölatif hıza sahip olduğunda taşıtın yere göre rölatif hızı havaya göre olandan farklıdır.

Taşıtın aerodinamiği incelenirken anlaşılması kolay olması için havanın hareketsiz olduğu ve taşıtın yere göre sabit bir rölatif hızla hareket ettiği düşünülür. Aynı zamanda taşıt hızının havanın sıkıştırılamaz özellikte incelenebilmesini sağlayacak kadar düşük olması ve taşıtın düz bir yolda ilerlediği kabulleride yapılmalıdır.

Aerodinamik analizlerde dikkat edilmesi gereken diğer bir nokta; taşıtın sabit hava içinde hareket etmesi ile (hava tünellerinde olduğu gibi) havanın sabit taşıt üzerinden hareket etmesinin hiçbir farkı olmadığıdır. Bütün aerodinamik fenomenler taşıt ile havanın birbirine göre yaptığı rölatif hareketten kaynaklanmaktadır.

Herhangi bir anda taşıtın belirli bir noktasından geçen hava partikülünü düşünelim. Bu partikül hareket eden taşıta göre yerleştirilmiş bir koordinat eksenine göre rölatif bir hareket yapmaktadır ve belirli bir yol izlemektedir. Partikülün izlediği bu yola akışyolu denir. Daha sonda taşıt üzerinde belirlenen bu noktaya gelen diğer tüm partiküllerde bir önceki partikülün izlediği yolu izleyecektir. Bunun gibi diğer bütün akışyollarının oluşturduğu aileye taşıt çevresindeki hava akış şekli denir. Bu akış şekli taşıtın şekline ve hızına bağlıdır. Taşıt üzerindeki bu hava akış şekli rüzgar tünellerinde veya tüm taşıt yüzeyine ince ve esnek iplikler yerleştirilerek görüntülenebilir. Şekil 2.9'da normal boyutlardaki bir Volkswagen otomobilin üzerindeki hava akış şeklinin rüzgar tünelinde duman kullanılarak görüntülenmesi gösteriliyor.

Şekil 2.9: Rüzgar tünelinde taşıt üzerindeki akış şeklinin belirlenmesi için deney yapılırken.

Henüz taşıtın hareket alanına girmemiş hava akımları paralel ve durgun durumdadır, fakat hareket alanı içindekiler oldukça kompleks hareket durumları sergilerler. Dolayısyla taşıtın çevresinde deforme olmuş bir hava akımı vardır. İnceleme amacıyla kabullerini yaptığımız hava partikülünün hareketi incelendiğinde deforme olmamış bölgedeki partikülün taşıt ile eşit rölatif hıza sahip olduğunu görürüz. Fakat deforme olmuş bölgede (taşıt çevresinde) pürtikülün rölatif hızı bazen taşıt hızından yavaş bazen de hızlı olacak şekilde oldukça değişmektedir.

 2.2.1.2 Aerodinamik Kuvvetin Orijini

Enerjinin korunumu yasasından oldukça iyi bilinen bir formül olan Bernoulli’nin Teoremini çıkartabiliriz. Bu formül aynı akışyolu’nun her noktasındaki atmosferik ve dinamik basınçların toplamının sabit olacağını gösterir. Atmosferik basınç P, dinamik basınç q=r V²/2 ve toplam basınç H ile gösterilirse aerodinamiğin temel yasası

[2.3] 

şeklinde oluşur. Buradaki toplam basınç henüz taşıtın hareket alanına girmemiş yani deforme olmamış hava ortamından hesaplanabilir. Bu formül bize havanın hızının değiştiği yerlerde dinamik basıncında değişeceğini gösterir. Bernoulli’nin Teoreminden anlaşılacağı üzere hareketi halindeki bir taşıtın çevresinde oldukça spesifik bir basınç dağılımı oluşur.

Bu basınçlar taşıtın dış yüzey alanına göre integre edilirse, taşıtın üzerinde, rölatif hızdan dolayı oluşan bileşke aerodinamik kuvvet bulunur. Bu kuvvet aslında taşıt yüzeyindeki bir yayılı kuvvettir, fakat hesaplamalarda kolaylık olması için bu basınç kuvvetlerinin taşıt üzerindeki belirli bir noktadan etkidiği şeklinde bir idealleştirme yapılabilir. Bu noktaya basınç merkezi (center of pressure, c. p. ) denir. Şekil 2.10. Bu nokta ağırlık merkezi (center of gravity, c.g. ) ile aynı nokta değildir. Fakat bu iki noktanın çakıştırılması oldukça büyük faydalar sağlar.

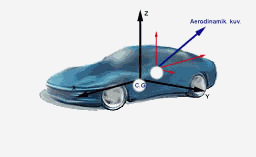
Şekil 2.10: Basınç merkezi ve ağırlık merkezinin konumları.

Yukarıda belirtilen integralin sonucunda aerodinamik kuvvetin hızın karesiyle, hava akımına karşı gelen taşıt alanıyla ve birimsiz bir katsayı ile orantılı olduğu görülür ve aşağıdaki şekilde yazılabilir.

[2.4]

burada;

q; dinamik basınç

A; karakteristik taşıt alanı

C_D; aerodinamik direnç katsayısıdır.

Bileşke aerodinamik kuvvet analizlerde kolaylık olması için üç bileşene ayrılabilir:

1. Yere paralel ve taşıtın ileri hareket yönüne zıt, aerodinamik çeki kuvveti; DA
2. Taşıt hareket doğrultusuna ve yere dik aerodinamik kaldırma kuvveti, LA
3. Havanın hareketi taşıt şekline göre simetrik olmadığı zamanlarda oluşan aerodinamik kuvvetin yan bileşeni, YA. Bu kuvvet bileşeni diğer iki bileşen ile de dik açı yapmaktadır.

Aerodinamik kuvvetin bu bileşenleri aşağıdaki şekilde hesaplanabilir:

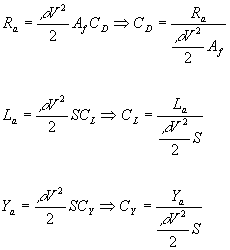[2.5]

burada;

C_D; aerodinamik direnç katsayısı

C_L; aerodinamik kaldırma katsayısı

C_Y; aerodinamik yan kuvvet katsayısı

A; taşıtın karakteristik alanıdır.

Yukarıda da belirtildiği gibi aerodinamik kuvvetlerin bileşkesinin etkidiği nokta olarak belirlediğimiz basınç merkezi ile taşıtın bütün dinamik analizlerinin yapıldığı nokta olan ağırlık merkezi aynı nokta değildir. Aerodinamik kuvvetlerinde taşıt dinamiğine etkisi hesaplanmak istendiğinde bu kuvvetlerin de ağırlık merkezine taşınması gereklidir. Bu durumda dinamik analizin içine aerodinamik momentler girmektedir. Bu momentler aerodinamik kuvvetler ile bunların ağırlık merkezine olan uzaklıklarının çarpımı ile bulunabilir. Şekil 2.11.

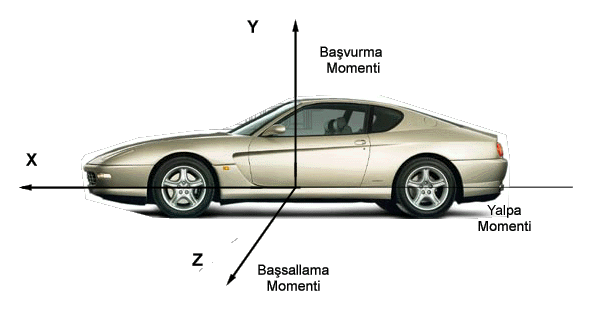
Şekil 2.11: Taşıt üzerinde eksenlerin yerleşimi ve eksenlere göre momentler.

Aerodinamik kuvvetler üç bileşene ayrıldığına göre bunların ağırlık mertezine taşınması sonucunda üç aerodinamik moment oluşur. Bunlar:

1. Aerodinamik çeki ve aerodinamik kaldırma kuvvetlerinden kaynaklanan baş sallama momenti M_A dır. Basınç merkezinin ağırlık merkezine göre rölatif pozisyonu xc ve zc uzaklığında olarak tanımlanırsa;

   [2.6] olur.

   Burada L taşıtın karakteristik uzunluğudur ve binek taşıtlar için genellikle ön ve arka akslar arasındaki uzunluk alınır. C_M ise birimsiz baş sallama momenti katsayısıdır.

2. Aerodinamik devrilme momenti N_A, x_c uzaklığında etkiyen aerodinamik yan kuvvette kaynaklanmaktadır.

   [2.7]

   burada C_N birimsiz devrilme momenti katsayısıdır.

3. Aerodinamik yuvarlanma momenti Q_A, z_c uzaklığında etkiyen aerodinamik yan kuvvetten kaynaklanmaktadır.

   [2.8]

burada C_Q birimsiz yuvarlanma momenti katsayısıdır.

Taşıt endüstrisinde bütün bu aerodinamik katsayıların maksimum kesit alanı ile ilgili olduğu kabul edilmektedir. Bu alan pratik olarak taşıtın ön kesit alanı ile aynıdır ve genellikle referans alanı veya karakteristik alan olarak adlandırılır. Şekil 2.12.

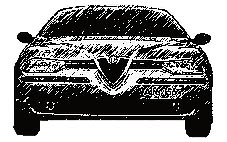
Şekil 2.12: Taşıtın kesit (referans) alanı.

Bu alan lastiklerin hava akımına karşı olan alanlarınıda kapsar. Bu alan bazen ön kesit alanı olarak adlandırılır, çünkü bu alan aslında yaklaşık olarak göz ile görülebilir olan veya küresel açı etkilerni ihmal edebilecek kadar uzak bir mesafeden fotoğraf makinası (veya kamera) ile görüntülenen alandır. 

2.2.2 Aerodinamik Kuvvetin Performansa Etkisi

Halk arasındaki genel kanı aerodinamik kuvvetlerin taşıt performansını fazla etkilemediği yönündedir. Hatta bazı kişiler taşıtlara verilen aerodinamik biçimlerin sadece çekici göstermek amacıyla yapıldığını düşünmektedir. Bu düşüncelerin doğruluğunun araştırılması için aerodinamik kuvvetlerin taşıt hareketi üzerindeki etkileri incelenmelidir. Bu analizi kolaylaştırmak için taşıtın sabit bir hız ile düz bir yolda ilerlediğini ve atmosferde rüzgar olmadığını düşünelim. Böylece taşıt üzerindeki bütün kuvvetler dengededir ve taşıtın dik simetri ekseninde etki etmektedirler, yani hiçbir yan kuvvet yoktur.

Taşıtın yukarıda bahsedilen şekilde hareketi sırasında aerodinamik çeki ve aerodinamik kaldırma bileşenlerine ayrılabilen aerodinamik kuvvetlerin yanı sıra tekerleklerdeki yuvarlanma direnç kuvvetininde dikkate alınması gereklidir. Çünkü çeki tekerleklerinde giden tork hem aerodinamik kuvvet hem de yuvarlanma direnci ile dengelenmektedir.

Aslında aerodinamik kuvvet ile yuvarlanma direnci birbiriyle oldukça kompleks bir şekilde bağlantılıdır. Aerodinamik kaldırma kuvveti yukarı doğru ise bu kuvvet taşıtın zemine uyguladığı normal kuvveti azaltır ve dolayısıyla yuvarlanma direncini de azaltır. Bu durumun tersi olan aerodinamik kaldirma kuvvetinin aşağı doğru olması durumunda da yuvarlanma direnci artar. Bu durum aşağıdaki şekilde ifade edilebilir:

[2.9]

Taşıtın belirtilen yol durumundaki toplam direnci R, aerodinamik çeki kuvveti ve yuvarlanma direnç kuvveti toplanarak bulunabilir.

[2.10]

Daha öncede belirttiğimiz gibi taşıt sabit hızla hareket ettiği için üzerindeki bütün kuvvetler dengededir. Öyleyse toplam direnç kuvveti aktarma organları ve çeki tekerleri aracılığıyla motordan sağlanan çeki kuvvetine, F_T, eşittir.

Aktarma organları ve vites kutusu ile ilgili olayları bir kenara bıraktığımızda, çeki kuvveti verilen hızdaki motor gücü ile direk bağlantılıdır. Bu durumda sağlanan güç:

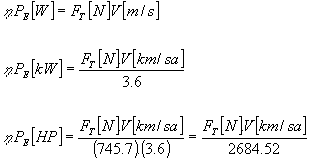[2.11] olur.

Burada h ; aktarma organlarındaki kayıplardan dolayı gelen verim ifadesidir.

Bu denklem motor tarafından sağlanan güç ile dirençler tarafından harcanan gücün eşitliğini göstermektedir. Bu durumda

[2.12]

burada aerodinamik kuvvet ile ilgili güç terimi;

[2.13]

yuvarlanma direnci ile ilgili güç terimi;

[2.14]

Bu iki denklem karşılaştırıldığında 2.13 denleminden aerodinamik gücün hızın küpü ile orantılı olduğu halde 2.14 denkleminden mekanik gücün hız ile direk orantılı olduğu görülür. Bu denklemlerin eğrileri çizilirse Şekil2.14 elde edilir. Bu eğrilerden de görüleceği üzere düşük hızlarda (binek otolar için 60- 70 km/sa) mekanik direnç gücü ile aerodinamik direnç gücü hemen hemen aynı olmakla birlikte yüksek hızlarda aerodinamik direnç gücü çabuk bir tırmanışa geçerek mekanik direnç gücünün oldukça üstüne çıkar. Bu arada mekanik direnç gücü yaklaşık olarak hız ile doğrusal bir seyir gösterir.

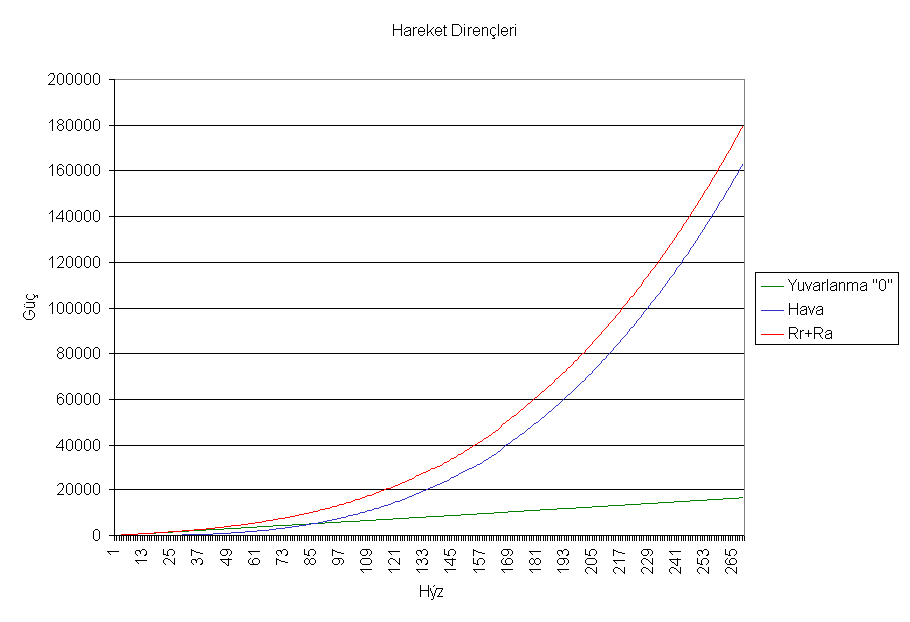
Şekil 2.13: Yuvarlanma direnç güç ve aerodinamik direnç güç eğrileri.

Şekil 2.14 deki grafikte toplam direnç gücü ile motor gücü eğrilerinin kesiştiği nokta taşıt üzerindeki kuvvetlerin dengede olduğu noktadır. Bu nokta o andaki vites seçimi ve gaz kelebeğinin açıklığına göre ulaşılabilecek maksimum taşıt hızıdır. Bu nokta genellikle motor gücü eğrisinin zirve noktasından daha ileride bir yerde olması istenir ve bu şekilde dizayn edilir. Böylece düşük hızlarda ivmelemek için bir miktar güç kalması sağlanmış olur.

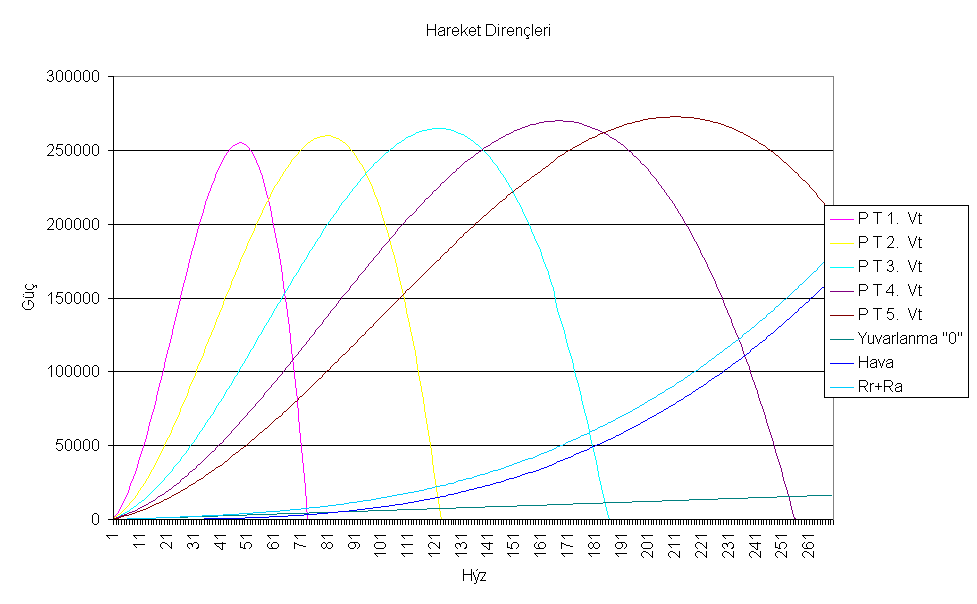
Şekil 2.14: Motor gücü ve aerodinamik güç eğrilerinin kesiştirilmesi.

2.2.2.1 Aerodinamik Kuvvet ve Maksimum Hız

Eğer maksimum motor gücü, maksimum taşıt hızında gerçekleşiyorsa, sağlanan maksimum güç taşıt ihtiyacı olan güce eşittir. Bu durumda denklem 2.11,2.13,2.14’den

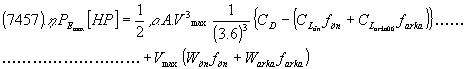[2.15]

Taşıtın ön ve arka lastikleri için yuvarlanma direnç katsayıları eşit kabul edilirse, yani f_ön=f_arka=f ise;

[2.16] olur.

Bu denklemin çözümü oldukça basittir ve taşıt endüstrisinde gösterimi genellikle grafik olarak yapılır. Maksimum taşıt hızının yaklaşık çözümü motor gücünün %70 olduğu durum için en uygundur ve aşağıdaki şekilde çözülürse;

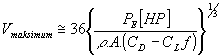[2.17] olur.

Eğer maksimum güçteki motor torku, vites oranları ve çeki tekerleklerinin etkin yarıçapları biliniyorsa, çeki tekerlerindeki kuvvet bulunabilir. 2.10 denkleminden taşıt maksimum hızı maksimum motor gücündeki çeki kuvveti, aerodinamik direnç kuvveti ve yuvarlanma direnç kuvveti cinsinden bulunabilir.

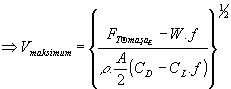[2.18]

Denklem 2.17 ve 2.18 aerodinamik direncin taşıt hızına olna etkisinin incelenmesinde kullanılır. Denklemlerden de görülebileceği gibi belirli motor gücü ve taşıt ağırlığında hız sadece yuvarlanma direç katsayısına değil, aerodinamik direnç katsayısı ve aerodinamik kaldırma katsayısına da bağlıdır. Taşıtın aerodinamik direnç katsayısı veya referans kesit alanı azaltılarak elde edilebilir maksimum taşıt hızı arttırılabilir. Aerodinamik direnç kuvvetlerinin düşürülmesinin avantajlarından tam anlamıyla yararlanmak istiyorsak, taşıtın aktarma organlarındaki dişlilerin yeniden ayarlanması gerekmektedir.

Aerodinamik kaldırma kuvvetinin taşıt hızına olan etkisi biraz daha karışıktır. 2.17 ve 2.18 denklemlemlerinden aerodinamik kaldırma kuvvetinin (pozitif yönde) arttırılması yuvarlanma direncini azaltır ve dolayısıyla maksimumu taşıt hızını arttırır. Diğer taraftan aerodinamik kaldırma kuvveti üretilebilecek maksimum çeki kuvvetini de etkilemektedir. Bu kuvvet çeki lastiklerinin yola tutunması ile ilgilidir:

[2.19]

Burada m yolun adezyon sınırıdır. Bu katsayı yol yüzeyinin yapısı, lastiğin diş şekli ve lastik dişlerinin malzemesiyle ilgilidir. Aerodinamik kaldırma kuvvetinin artması taşıtın üretebileceği maksimum çeki kuvvetini azaltır ve bu değeri motorun üretebileceği değerin de altına indirebilir. Bu durumda aerodinamik kaldırma kuvvetinin taşıt üzerindeki iki etkisi birbiriyle çakışmaktadır. Ortalama bir binek taşıt için pratikte bu etkilerin bir anlamı yoktur. Fakat hızlı spor arabalar ve yarış araçları için bu etkiler çok önemlidir ve negatif kaldırma aygıtları kullanılarak çeki kuvvetini arttırmak daha baskın bir uygulamadır. Aerodinamik kaldırma kuvvetinin etkileri yol tutuş ve yönlendirme sistemleri üzerinde de oldukça etkilidir. 

2.2.2.2 Aerodinamik Direncin Yakıt Tüketimine Etkisi

Aerodinamik direnç kuvveti motorun sağladığı çeki kuvveti ile karşılanmaktadır. Onun için direnç kuvveti direk olarak grekli motor gücüne ve dolayısıyla da yakıt tüketimine etkilidir. Herhangi bir hızdaki yakıt tüketi direk olarak gerekli olan güç ile orantılıdır. Aerodinamik direnci yenmek için gerekli güç te motor gücünün büyük bir kısmını oluşturmaktadır.

Bu konunun önemini daha iyi anlamak için ülke genelindeki yakıt tüketiminin ve bunun ekonomiye olan etkisinin incelenmesi gereklidir. Şu anda Türkiye’de 3 milyon taşıt olduğunu kabul edelim. Bütün bu taşıtların ortala hızının 55 km/sa olduğu ve senede ortalama 8000 km mesafe katettikleri kabullerinide yapalım. Eğer taşıtlar bu şartlarda çalışırken ortalama 30 HP motor gücü ürettikleri ve bu hızdaki ortalama yakıt tüketiminin 9 km/sa olduğu kabulleri ile hesap yapıldığında, yıllık ortalama yakıt tüketimi 888 milyon litre olur. Taşıt dizaynındaki bazı iyileştirmelerle aerodinamik direnç katsayısı ortalama %2 düşürülebilir. Katsayıdaki bu düşüş motor gücü ihtiyacına %0.5 olarak yansımaktadır. Bunun ekonomik anlamı ise; yakıt tüketiminde senelik 4.5 milyon litre yakıt tasarrufu ve 15.01.1999 tarihi fiyatlarıyla 3.2 milyon USD, 1 tirilyon TL demektir.

Taşıtların karakteristik yakıt tüketimi genellikle deneysel yollarla bulunur ve 1 HP için gerekli değer olan C [lt/HP.sa] olarak belirtilir. Bu katsayının gerçek motor gücü ile çarpımı motorun toplam karakteristik yakıt tüketimini verir:

[2.20]

Pratikte yakıt tüketimi lt/km veya km/lt gibi oranlar şeklinde verilir. Avrupanın çoğunluğunda ve Türkiye’de 100 km mesafede tüketilen yakıt miktarı verilmekle birlikte İngiltere ve diğer bazı ülkelerde 1 lt yakıt ile katedilecek mesafe verilmektedir.

Aerodinamik karakteristiğin yakıt tüketimine etkisini incelemek için taşıtın tavanına bir bagaj yerleştirildiği durumu düşünelim. Bu durumda taşıtın aerodinamik direnç katsayısında D C_D kadarlık bir artış olur ve toplam direnç katsayısı C_D+D C_D olur.

Tavanında bagaj olan tşıt aynı hızda normalden daha fazla motor gücüne ihtiyaç duyar. 2.13 nolu denklemi kullanarak bagajlı ve bagajsız durum için gerekli olan güçleri hesaplayıp oranlarsak;

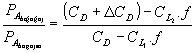[2.21] 

ifadesi ortaya çıkar. Buradaki CL1 ve CL2 bagaj yerleştirilmeden önceki ve bagajlı durumdaki aerodinamik direnç katsayılarıdır. Karakteristik yakıt tüketiminin gaz kelebeği açıklığına göre değişmediği kabul edilirse;

[2.22] olur.

Bu örnek belirli bir mesafe için taşıtın dizaynı iyileştirilerek aerodinamik direnç katsayısında elde edilecek azalmanın yakıt tüketimini seyir hızının karesiyle orantılı olarak azaltacağını gösterir. 2.22 nolu denklemi taşıtın ağırlığının azaltılması veya lastiklerin yuvarlanma direnç katsayılarının azaltılmasının da yakıt tüketimini azaltacağını gösterir.

Yukarıdaki örnekte karakteristik yakıt tüketiminin gaz kelebeğinin açıklığıyla değişmediği kabulü yapılmıştı, oysaki gerçekte oldukça değişmektedir. Çeşitli gaz kelebeği açıklıklarına göre karakteristik yakıt tüketiminin hesabı oldukça zor ve karmaşık bir iştir. Bunun için taşıt üreticileri ve ülkelerin hükümetleri belirli hızlardaki karakteristik yakıt tüketimi değerlerinin hesaplanıp belirtilmesini kararlaştırmışlardır. Otomobil kataloglarına bakılınca görülebileceği gibi karakteristik yakıt tüketimi genellikle 90 km/sa sabit hızda, 120 km/sa sabit hızda ve şehir içi trafiğinde değişken hızda verilmektedir.

Taşıt üzerindeki dirençlerin herbirinin yakıt tüketimine olan etkileri harcadıkları güçlerle orantılıdır. Bunun için şehir içinde ortalama 30 km/sa hızla seyahat eden bir taşıtın inceleyecek olursak; en çok taşıtı ivmelendirmek için iş yapılır ve bu iş daha sonra frenlerden ısı olarak atılır. Bu sırada yuvarlanma direncine ve aerodinamik dirence karşı da iş yapılır. Eğer M kütlesindeki bir taşıt durgun halden V hızına çıkartılırsa yapılan iş;

[2.23] dir.

Bu sırada s kadar yol katedildiyse yuvarlanma direncine karşı yapılan iş (aerodinamik kaldırma kuvveti=0 için)

[2.24] dir. 

Aynı mesafe için aerodinamik direnç kuvvetine karşı yapılan iş ise;

[2.25] dir.

Bu hareket şartlarını 750 kg ağırlığındaki bir taşıtın seyahat sırasında maksimum 50 km/sa hız yaptığı, 25 km gittiği ve bu arada 30 defa durduğu şeklinde bir duruma uyarlarsak; yuvarlanma direnç katsayısı 0.02 ve referans alanı 1.8 için

E1 : E2 : E3 = 1.2 : 2.0 : 1.0 oranını buluruz.

Bu oran şehir içinde olduğu gibi düşük hızlarda motorun kullanılabilir iş kapasıtesinin ¼’ü aerodinamik dirence ve ¾’ünün mekanik direnci yenmek için harcandığı görülür.

Eğer aynı yolculuk 90 km/sa maksimum hız ile iki defa durarak katedilseydi bu oran:

E1 : E2 : E3 = 0.3 : 2.0 : 3.9 olurdu. Bu durumda otoyol gibi hız sınırının yüksek olduğu kısımlarda motorun kullanılabilir iş kapasitesinin yaklaşık 2/3’ü aerodinamik direnç kuvvetine karşı harcanıyor.

2.2.2.3 Aerodinamik Direnç Kuvvetlerinin İvmelenmye Etkisi

Otomobil kataloklarına baktığımızda çoğunda taşıtın belirli bir hıza (genellikle 100 km/sa) ne kadar sürede ulaştıkları verilir. Taşıtın bu karakteristik özelliği sadece yarışlarda değil, diğer bir taşıtı sollama gibi günlük kullanımlarda da önemlidir.

Belirli bir gaz kelebeği açıklığı için motorun ürettiği tork belirli bir aralıkta hemen hemen sabittir. Bundan dolayı belirlenen bir dişli oranı (vites) için tekerleklerdeki tork bir hız aralığında sabit kabul edilebilir. Vites değiştirmek sadece terlekteki torku değiştirir, motor torkuna etkisi yok denecek kadar azdır.

Bu fiziksel kabulleri yaptıktan sonra taşıtı ivmesini hızın zamana göre türevi olarak hesaplarsak, M kütleli taşıtın ivmesi direnç kuvvetlerinden arta kalan çeki kuvveti ile ilişkiliendirilebilir. 2.10 denklemi kullanılarak aşağıdaki denklem çıkartılabilir.

[2.26]

Denklemdeki değişken sayısı oldukça fazla olduğundan çözümü grafik yoluyla yapmak en iyi görsel sonuçları verir.

Bu denklem incelendiğinde taşıtın ağırlığı arttıkça aynı çeki kuvveti içinn ivmesinin ezaldığı görülebilir. Aslında buradaki T/M değeri taşıtın güç/ağırlık oranıyla aynı anlamdadır ve bu oranın en iyi değeri tam gaz açıklığında elde edilir.

Aerodinamik direncin taşıt ivmesine etkisini görmek için aeroinamik direnç katsayısının C_D’den C_D+D C_D’ye çıktığını düşünelim. Bu durumda V hızındaki ivme değişimi;

[2.27]olur.

V₁ hızından V₂ hızına ivmelenme süresince geçen zamanı bulmak için 2.26 denkleminden faydalanılabilir. İvmelenme süresi “t” ivmenin (çarpmaya göre) tersi olduğuna göre (dV/dt)^-1’in grafiğini çizip V₁, V₂ ve grafikle sınırlı alanı hesaplarsak bu değeri bulabiliriz. Bu problemin detaylı analizi ivmelenme süresinin taşıtın ağırlığı ve aerodinamik direnç katsayısındaki artışla arttığını göstermiştir. Buna göre zamandaki artış;

[2.28] olur.

Belirli hızlar arasındaki ivmelenme süresi önemli olduğu gibi bazen de mesafe sınırlayıcı etkendir. Bunun için ivmelenmeyle mesafe arasında bir ilişki kurmak gereklidir. İveme ifadesini (V.dV/ds) olarak yazıp 2.26 denkleminde yerine koyarsak

[2.29] olur. 

Zaman ile mesafe hızla orantılı olduğundan (dV/dt)-1 ‘in hızın karesine göre (V2) grafiği çizilip V1, V2 ve grafikle sınırlı alanı hesaplarsak gerekli yol uzunluğunu bulabiliriz. Buna rağmen eğer çeki kuvvetini sabit kabul edersek ve bu çeki kuvvetinde sıfır ivme ile elde edilen karakteristik taşıt hızını Vm ile gösterirsek

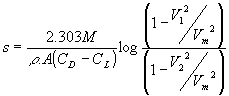[2.30] olur.

Yukarıdaki denklem dikkatlice incelendiğinde aerodinamik direnç katsayısındaki artışın verilen hıza ulaşmak için gerekli mesafeyi arttırdığı veya belirli bir mesafe icin ulaşılan hızı düşürdüğü görülebilir.